An Enhanced Non-Oscillatory BFECC Algorithm for Finite Element Solution of Advective Transport Problems

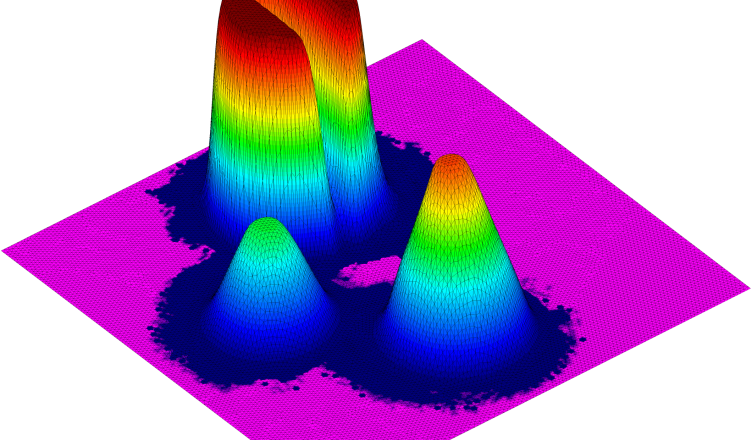
In this paper, the “back and forth error compensation correction (BFECC)” methodology is utilized to improve the solvers developed for the advection equation. The necessary requirement for obtaining a non-oscillatory solution is that the solver embodies discrete maximum principle DMP [1]. Therefore, strict obedience to DMP is enforced by incorporating a gradient-based limiter into the BFECC algorithm. The accuracy of the BFECC algorithm in capturing the steep-fronts in hyperbolic scalar-transport problems is improved by introducing a controlled anti-diffusivity. The performance of the proposed methodology is assessed by solving a series of benchmarks utilizing different combinations of the BFECC algorithms and the underlying numerical schemes.

 

[1] E. Burman, A. Ern, Nonlinear diffusion and discrete maximum principle for stabilized Galerkin approximations of the convection–diffusion-reaction equation, Comput. Methods Appl. Mech. Engrg. 191 (2002) 3833–3855, http://dx.doi.org/10.1016/S0045-7825(02) 00318-3, https://www.sciencedirect.com/science/article/pii/S0045782502003183.